Este post fez um exercício de previsão para o Impeachment brasileiro utilizando um modelo de regressão particionada através do uso de árvores. As previsões foram atualizadas diariamente e o resultado percentual se referia à proporção de Deputados a favor do Impeachment em relação a totalidade dos membros, considerando diferentes índices de ausência.

Com objetivos didáticos, publiquei o modelo no dia 1º de abril e foi o primeiro do gênero que apareceu na internet. Desde o início, as previsões indicavam grande probabilidade de o Impeachment passar pela etapa de julgamento de admissibilidade na Câmara com cerca de 70% a 75% de votos favoráveis, variando de acordo com a mudança dos dados/fonte. A última atualização do modelo e o resultado final podem ser vistos abaixo:

Previsão com dados do Vem Pra Rua

Ausência	0%	2,5%	5%	7,5%	10%
Estimativa final	71,73%	69,20%	69,00%	66,67%	64,91%
Resultado:	A favor	A favor	A favor	A favor	Contra

Dados obtidos em: 16/04/2016 às 16:00 (último arquivo aqui)

Resultado Final: 367 de 513 votos favoráveis -> 71,54% (A favor)

Taxa de ausência: 2 de 513 deputados -> 0,39%

Como pode ser visto, a estimativa final indicava cerca de 368 votos favoráveis com taxa próxima de 0% de ausência e o resultado final foi de 367 com taxa de ausência de 0,39%. Assim, apesar das limitações do modelo, ele fez um excelente trabalho em prever o resultado final do processo de Impeachment na Câmara brasileira.

O modelo, apesar de parecer complicado, intuitivamente é bem simples, ele apenas considerava a informação partidária e do Estado dos Deputados que já haviam manifestado voto e a partir daí construía uma árvore com as divisões entre partido e Estado para inferir sobre os votos dos indecisos. Muitas limitações foram levantadas a respeito do modelo, as quais, em boa parte, eu concordava. Um exemplo é o fato de ele não captar a barganha e o jogo político por trás das decisões. Entretanto, na semana que antecedeu o Impeachment, a dinâmica da definição dos votos acabou se dando primeiro através de uma deliberação dentro do partido e posteriormente pelo apoio dos Deputados à decisão da maioria, com apenas alguns dissidentes. Como o pressuposto do modelo era de que os Deputados seguiriam a orientação partidária, então ele acabou se mostrando bem eficaz na previsão dos votos. Também o Estado do Deputado teve um peso grande nas manifestações de voto. Afinal, parece que a política brasileira não era tão complicada de se entender!

Após a publicação, o modelo fez bastante sucesso entre estudantes e acadêmicos e acabou ganhando notoriedade na mídia. Conforme as atualizações eram feitas, novas notícias apareciam. Algumas repercussões foram:

Artigos em jornais

Entrevistas em rádios:

Rádio Bandeirantes

Rádio Jovem Pan SP

Rádio Canção Nova.

Sobre a votação no Senado, para a admissibilidade é necessário maioria simples, e para o julgamento é necessário 2/3. Decidi por enquanto não manter as atualizações da previsão para o Senado pelos seguintes motivos:

Já é praticamente certo que a votação terá maioria simples, pois já há manifestação de mais de 50% da Casa a favor do Impeachment;
Após a admissibilidade no Senado passar, a Presidente será destituída por 180 dias antes do julgamento final, o que é um grande período de tempo, podendo ocorrer muitos fatos políticos relevantes até lá;

Caso aparente ser necessário, poderei incluir algumas projeções para o Senado quando o julgamento se aproximar.

Após a publicação deste post, recebi inúmeras sugestões, contribuições e apoio. Gostaria de agradecer principalmente o empenho do Prof. Cláudio Shikida na divulgação, as sugestões dadas pelo Gabriel Torres, Prof. Bruno Speck, membros da comunidade de usuários do R, entre outras pessoas. Ao Fernando Barbosa por me disponibilizar os dados do Estadão através de uma macro em VBA, ao Adriano Filho por traduzir o meu script de coleta dos dados de Python para R. Ao Datafolha por me disponibilizar os dados antecipadamente para análise. E a todas as outras pessoas que ajudaram na divulgação do trabalho. Achei muito gratificante a repercussão que o post teve pois a maior parte dos trabalhos ou consultorias que aparecem na mídia não disponibilizam a metodologia ou as etapas para replicação das projeções feitas. Acredito que estamos em uma nova era da ciência, em que a produção de conhecimento deve estar aberta para o escrutínio do público, possibilitando assim a crítica detalhada do método, e com isso melhorando o resultado e objetivo final do exercício. Entendo que muitas pessoas somente lêem as manchetes, mas pelo menos desta vez havia um link nas reportagens que levava a este post, que mostra as etapas para replicação dos resultados obtidos. Para finalizar, obrigado a todos e aproveitem a leitura!

22 de abril de 2016

Regis A. Ely

Cenário do Impeachment

Nota: A Tabela acima contém a última atualização da previsão feita, mas o post abaixo, bem como todas as informações nele, são referentes a 1º de abril.

A favor ou contra? Parece que todo cidadão brasileiro já tem uma opinião formada sobre o Impeachment, com exceção dos políticos, que estão um tanto indecisos. O site vem pra rua fez um serviço de utilidade pública ao elencar a intenção de voto de todos os deputados e senadores brasileiros. Mas a verdade é que ainda resta muita dúvida sobre qual será o resultado dessa votação. Uma vez que os dados estão disponíveis, podemos tentar realizar uma tarefa quase impossível: prever qual será o desfecho da situação política brasileira. Para isso vamos utilizar um simples modelo de regressão baseado em árvores, implementado no pacote rpart do R. Primeiro vamos aos fatos:

Atualmente temos 513 deputados e 81 senadores no Brasil;
O processo de Impeachment pode ser dividido em duas etapas: o juízo de admissibilidade e o julgamento do impedimento;
Para o pedido ser admitido é necessário 2/3 de votos favoráveis na Câmara dos Deputados e 1/2 de votos favoráveis no Senado Federal;
Para o impedimento da Presidente é necessário 2/3 de votos favoráveis no Senado Federal;
Considerando os números, para termos um novo Presidente é necessário que 342 Deputados e 41 Senadores sejam favoráveis a admissibilidade, e que 54 Senadores sejam favoráveis ao impedimento (crédito ao Gabriel Torres por lembrar das recentes mudanças feitas pelo STF).

Para conhecer um pouco mais sobre o processo de Impeachment você pode ler a legislação.

Obtendo os dados

Como a política brasileira é mais imprevisível que episódio de Game of Thrones, vale a pena automatizar a coleta de dados para podermos atualizar constantemente a previsão - neste exato momento em que escrevo este post já ocorreram mudanças na intenção de voto de 2 Deputados. Para isso, escrevi um pequeno script em Python2.7 que coleta os dados do site vem pra rua e grava em um arquivo csv com o nome imp.csv, deixando-o pronto para ser analisado no R. Você pode ver este script aqui. Se estiver interessado em um script que faz o mesmo para R, você pode ver a versão feita pelo Adriano Azevedo Filho aqui.

Uma vez obtidos os dados podemos carregá-lo no R digitando:

data <- read.csv("imp.csv", sep = ";")

Aqui estão as primeiras 10 observações:

      Voto                   Nome Partido Estado Senador
A favor            Aecio Neves    PSDB     MG       1
A favor Aloysio Nunes Ferreira    PSDB     SP       1
A favor            Alvaro Dias      PV     PR       1
A favor             Ana Amelia      PP     RS       1
A favor      Antonio Anastasia    PSDB     MG       1
A favor       Ataides Oliveira    PSDB     TO       1
A favor           Blairo Maggi      PR     MT       1
A favor      Cassio Cunha Lima    PSDB     PB       1
A favor      Cristovam Buarque     PPS     DF       1
A favor          Dalirio Beber    PSDB     SC       1

A variável Voto contém três possíveis valores: “A favor”, “Contra” ou em branco (indecisos). Já a variável Senador é uma dummy que é igual a um quando o político é Senador e zero quando é Deputado. As outras três variáveis são o Nome, o Partido e o Estado.

Para prevermos o resultado do Impeachment vamos utilizar o método de regressão com particionamento recursivo, implementado pelo pacote rpart. A ideia é que podemos separar as decisões dos políticos em grupos baseados em seus Partidos e Estados. Esse método é ideal para o caso brasileiro, pois sabemos que existem cisões entre os partidos brasileiros dependendo do Estado.

Implementação do modelo

Uma vez carregados os dados na variável data, vamos ler o pacote rpart, criar algumas novas variáveis que serão úteis e fazer pequenos ajustes:

install.packages("rpart") # instale o pacote rpart caso não o tenha feito
library(rpart)

# Transforma os indecisos em NA
data[which(data$Voto == ''),"Voto"] <- NA
data$Voto <- droplevels(data$Voto)

# Cria variáveis para os senadores e deputados
senadores <- data[which(data$Senador == 1),]
deputados <- data[which(data$Senador == 0),]
n_sen <- nrow(senadores) # número de senadores
n_dep <- nrow(deputados) # número de deputados

# Separa deputados indecisos e decididos
train_dep <- na.omit(deputados) # deputados decididos
test_dep <- deputados[which(is.na(deputados$Voto)),] # deputados indecisos
train_sen <- na.omit(senadores) # senadores decididos
test_sen <- senadores[which(is.na(senadores$Voto)),] # senadores indecisos

Note que chamamos o conjunto dos Senadores e Deputados que já estão decididos de train, pois estes serão os dados utilizados para treinar nosso modelo. Posteriormente, aplicaremos os resultados do modelo nos dados denominados test, que é o conjunto dos políticos indecisos, e então teremos nossa previsão.

Para estimar o modelo digitamos:

# Estimação do modelo
formula = Voto ~ Partido + Estado # o voto é função do Partido e Estado
fit_dep = rpart(formula, method = "class", data = train_dep)
fit_sen = rpart(formula, method = "class", data = train_sen)
fit_dep
fit_sen

Ao avaliar os resultados da variável fit_dep, obtemos os nódulos de divisão para os Deputados:

n= 384 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

 1) root 384 119 A favor (0.69010417 0.30989583)  
   2) Partido=DEM,PEN,PHS,PMDB,PP,PPS,PR,PRB,PROS,PSB,PSC,PSD,PSDB,PSL,PTB,PTdoB,PTN,PV,REDE,SD 299  36 A favor (0.87959866 0.12040134)  
     4) Estado=AC,AL,DF,ES,GO,MG,MS,RJ,RO,RS,SC,SP 174   4 A favor (0.97701149 0.02298851) *
     5) Estado=AM,AP,BA,CE,MA,MT,PA,PB,PE,PI,PR,RN,RR,SE,TO 125  32 A favor (0.74400000 0.25600000)  
      10) Partido=DEM,PHS,PPS,PRB,PSB,PSC,PSD,PSDB,PSL,PV,REDE,SD 75   4 A favor (0.94666667 0.05333333) *
      11) Partido=PEN,PMDB,PP,PR,PROS,PTB,PTdoB,PTN 50  22 Contra (0.44000000 0.56000000)  
        22) Estado=AM,BA,CE,PE,PR,RN,TO 35  15 A favor (0.57142857 0.42857143)  
          44) Partido=PEN,PMDB,PR,PTB 20   5 A favor (0.75000000 0.25000000) *
          45) Partido=PP,PROS,PTdoB,PTN 15   5 Contra (0.33333333 0.66666667) *
        23) Estado=MA,MT,PA,PB,PI,RR,SE 15   2 Contra (0.13333333 0.86666667) *
   3) Partido=PCdoB,PDT,PSOL,PT 85   2 Contra (0.02352941 0.97647059) *> fit_dep

Parece complicado, mas uma maneira mais fácil de visualizar estes nódulos é graficamente. Para isso utilizamos a função plot no R. Para construirmos árvores mais bonitas utilizamos a função text com alguns argumentos especiais (digite ?plot.rpart no R para mais informações).

# Plota árvore dos deputados decididos
plot(fit_dep, uniform = TRUE,
     main = "Árvore do Impeachment - Câmara (decididos)", margin = 0.2)
text(fit_dep, use.n = TRUE, all = TRUE, cex = .8, pretty = TRUE,
     fancy = TRUE, minlength = 12, bg = "yellow")
mtext("Valores são: A favor/Contra", side = 1)

# Plota árvore dos senadores decididos
plot(fit_sen, uniform = TRUE,
     main = "Árvore do Impeachment - Senado (decididos)", margin = 0.2)
text(fit_sen, use.n = TRUE, all = TRUE, cex = .8, pretty = TRUE,
     fancy = TRUE, minlength = 12, bg = "yellow")
mtext("Valores são: A favor/Contra", side = 1)

Assim, obtemos os seguintes gráficos:

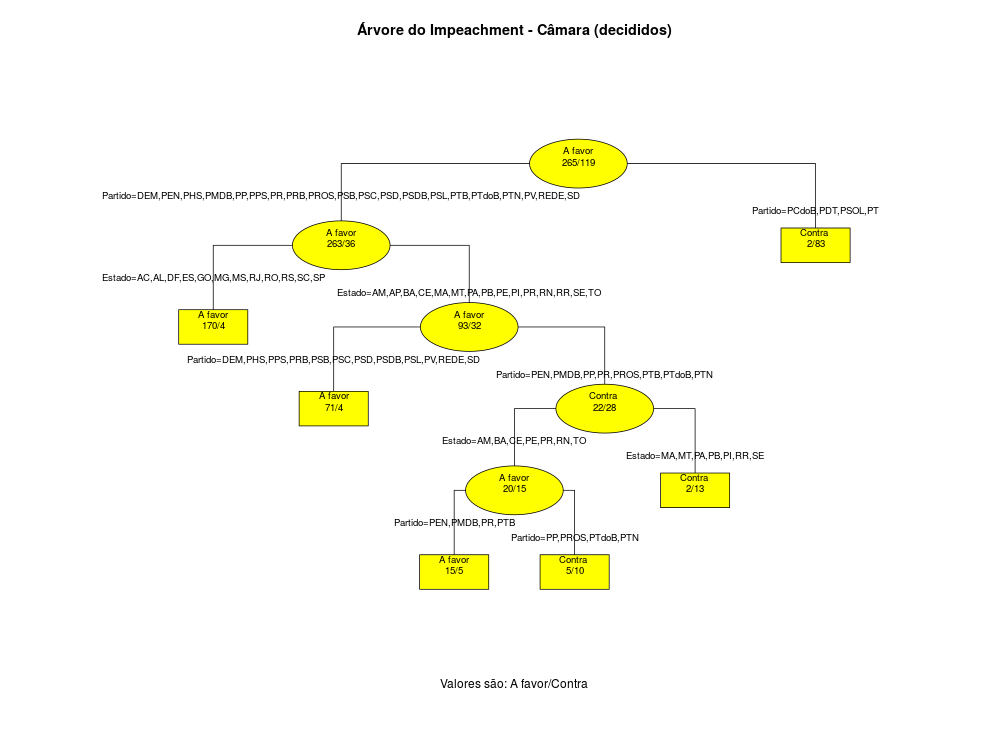
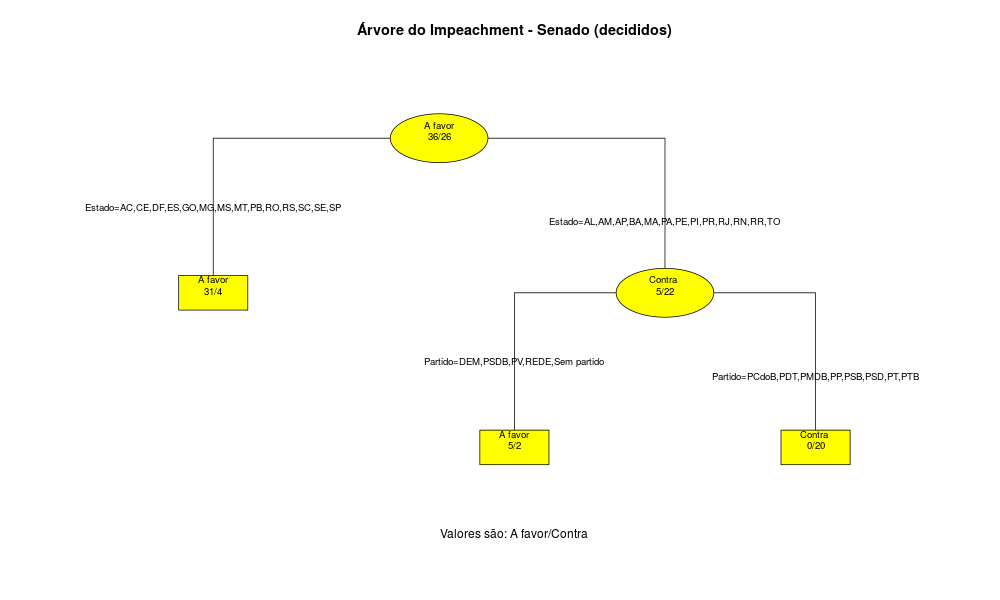
Ainda assim não é tão simples, mas quem disse que a política brasileira era fácil de entender. Vamos primeiro analisar o Congresso. Repare que no primeiro nódulo há uma divisão partidária, com o grupo PCdoB, PDT, PSOL e PT de um lado, sendo que 2 Deputados são a favor e 83 contra o Impeachment. No resto dos partidos, existem divisões de acordo com o Estado. No grupo AC,AL,DF,ES,GO,MG,MS,RJ,RO,RS,SC,SP temos 170 Deputados a favor e apenas 4 contra, mas no restante dos Estados há divisões partidárias e por região. Resumindo, me parece que os partidos estão mais rachados nos Estados do Nordeste. No Senado a divisão é mais simples e parece ser explicada bastante pelo Estado do Senador.

Previsão dos votos indecisos

Após estimar o modelo podemos calcular a acurácia do mesmo utilizando as funções printcp() e plotcp(). Uma maneira rápida de obter a acurácia do modelo no conjunto train é digitando:

# Acurácia no conjunto train para Deputados
prev_class_dep <- table(predict(fit_dep, type="class"), train_dep$Voto)
sum(diag(prev_class_dep))/sum(prev_class_dep)

# Acurácia no conjunto train para Senadores
prev_class_sen <- table(predict(fit_sen, type="class"), train_sen$Voto)
sum(diag(prev_class_sen))/sum(prev_class_sen)

O resultado é:

[1] 0.9402597 # Deputados
[1] 0.9032258 # Senadores

Entretanto, ao utilizar uma estrutura muito complicada para o nosso modelo, podemos acabar cometendo o erro de overfitting em nossa previsão. Para evitar isso, devemos verificar qual a estrutura de árvores que gera o menor erro de previsão em um conjunto independente, chamado cross-validated. Para obter a acurácia do modelo de previsão nesse conjunto no caso dos Deputados podemos utilizar a informação da função printcp(fit_dep):

Classification tree:
rpart(formula = formula, data = train_dep, method = "class")

Variables actually used in tree construction:
[1] Partido

Root node error: 119/385 = 0.30909

n= 385 

       CP nsplit rel error  xerror     xstd
1 0.67227      0   1.00000 1.00000 0.076197
2 0.02521      1   0.32773 0.35294 0.051404

O taxa de erro do conjunto cross-validated (10-fold) pode ser obtida multiplicando-se o Root node error pelo menor valor do xerror, que corresponde ao melhor modelo. Assim, obtemos um erro de 0.1090902, o que nos dá uma acurácia de 0.8909098. No código abaixo faço a seleção automática do modelo com menor erro no conjunto cross-validated e estimo-o novamente com a função prune.

# Seleção do modelo com menor erro
fit_dep <- prune(fit_dep,
                 cp = fit_dep$cptable[which.min(fit_dep$cptable[,"xerror"]),
                                      "CP"])
fit_sen <- prune(fit_sen,
                 cp = fit_sen$cptable[which.min(fit_sen$cptable[,"xerror"]),
                                      "CP"])

Uma vez obtido o modelo com o menor erro, podemos utilizar os dados referentes aos parlamentares indecisos para realizar a previsão do voto e calcular o percentual de votos a favor com essas novas previsões:

# Previsão do modelo
prev_dep <- predict(fit_dep, test_dep, type = "class")
prev_sen <- predict(fit_sen, test_sen, type = "class")

# Previsão do percentual de votação a favor
n_dep_favor <- nrow(train_dep[which(train_dep$Voto == "A favor"),])
n_sen_favor <- nrow(train_sen[which(train_sen$Voto == "A favor"),])
n_dep_favor_prev <- length(which(prev_dep == "A favor"))
n_sen_favor_prev <- length(which(prev_sen == "A favor"))
percentual_dep <- (n_dep_favor + n_dep_favor_prev)/n_dep
percentual_sen <- (n_sen_favor + n_sen_favor_prev)/n_sen
percentual_dep
percentual_sen

E o resultado será:

[1] 0.7465887 # Câmara dos Deputados
[1] 0.5308642 # Senado Federal

Parece que na situação atual, o Impeachment passa pela etapa de admissibilidade mas esbarra no julgamento do Senado Federal.

Árvores com previsão

Para finalizar, vamos construir a árvore final que inclui os indecisos e utiliza o modelo simplificado com menor erro de previsão:

# Altera os dados originais para incluir a previsão dos indecisos
new_dep <- deputados
new_dep[names(prev_dep), "Voto"] <- prev_dep
new_sen <- senadores
new_sen[names(prev_sen), "Voto"] <- prev_sen

# Constrõe a árvore com os indecisos
fit_dep_prev = rpart(formula, method = "class", data = new_dep)
fit_sen_prev = rpart(formula, method = "class", data = new_sen)

# Plota a árvore dos Deputados com os indecisos
plot(fit_dep_prev, uniform = TRUE,
    main = "Árvore do Impeachment - Câmara (com previsão de indecisos)",
    margin = 0.2)
text(fit_dep_prev, use.n = TRUE, all = TRUE, cex = .8, pretty = TRUE,
     fancy = TRUE, minlength = 12, bg = "yellow")
mtext("Valores são: A favor/Contra", side = 1)
mtext(paste0("Percentual previsto a favor: ",
             round(percentual_dep*100, digits = 2), "%"))

# Plota a árvore dos Senadores com os indecisos
plot(fit_sen_prev, uniform = TRUE,
    main = "Árvore do Impeachment - Senado (com previsão de indecisos)",
    margin = 0.3)
text(fit_sen_prev, use.n = TRUE, all = TRUE, cex = .8, pretty = TRUE,
     fancy = TRUE, minlength = 12, bg = "yellow")
mtext("Valores são: A favor/Contra", side = 1)
mtext(paste0("Percentual previsto a favor: ",
             round(percentual_sen*100, digits=2), "%"))

O resultado está abaixo:

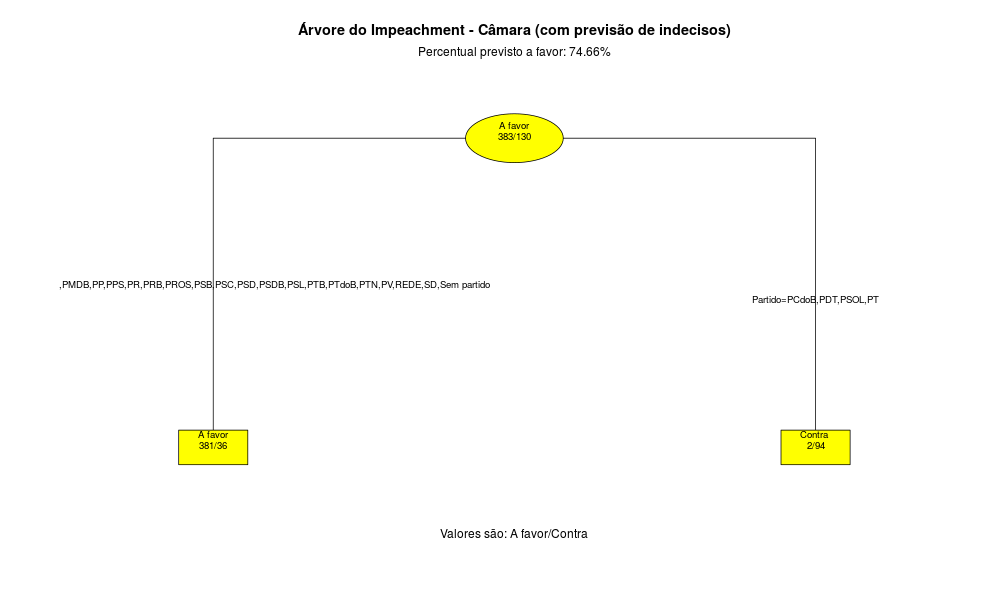
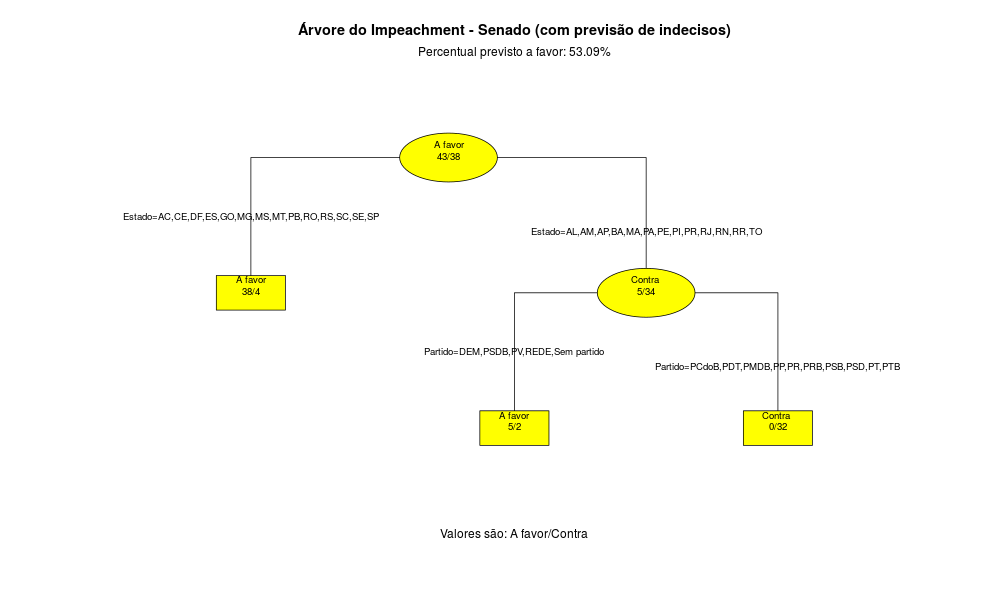
A árvore do Senado Federal nos mostra que a maior resistência ao Impeachment parece ser os partidos do PCdoB, PDT, PMDB, PP, PR, PRB, PSB, PSD, PT e PTB nos Estados AL, AM, AP, BA, MA, PA, PE, PI, PR, RJ, RN, RR, TO. O Impeachment precisa de 54 votos no Senado. Atualmente existem 36 Senadores com intenção de voto a favor e 26 contra. Assim, são necessários 18 votos dos 19 indecisos para a Presidente ser destituída do Cargo, ou então uma mudança no voto dos Senadores que se declararam contra o Impeachment.

Podemos visualizar a lista dos Senadores indecisos segundo o site vem pra rua com o comando:

senadores[which(is.na(senadores$Voto)), ]

O resultado nos dá:

<NA>             Acir Gurgacz         PDT     RO       1
<NA> Antonio Carlos Valadares         PSB     SE       1
<NA>            Ciro Nogueira          PP     PI       1
<NA>       Delcidio do Amaral Sem partido     MS       1
<NA>           Douglas Cintra         PTB     PE       1
<NA>            Elmano Ferrer         PTB     PI       1
<NA>  Fernando Bezerra Coelho         PSB     PE       1
<NA>               Helio Jose        PMDB     DF       1
<NA>       Joao Alberto Souza        PMDB     MA       1
<NA>            Jose Maranhao        PMDB     PB       1
<NA>              Lucia Vania         PSB     GO       1
<NA>         Marcelo Crivella         PRB     RJ       1
<NA>                Omar Aziz         PSD     AM       1
<NA>            Raimundo Lira        PMDB     PB       1
<NA>            Roberto Rocha         PSB     MA       1
<NA>                  Romario         PSB     RJ       1
<NA>              Romero Juca        PMDB     RR       1
<NA>             Sandra Braga        PMDB     AM       1
<NA>         Vicentinho Alves          PR     TO       1

Lidando com os ausentes

A ausência ou a abstenção pode trazer uma influência grande no resultado da votação, visto que o cálculo do percentual é feito sobre a totalidade dos membros e não apenas sobre os presentes (crédito ao Prof. Bruno Speck da USP por lembrar disto). Assim, decidi fazer uma simulação com diferentes taxas de ausência/abstenção, onde os deputados e senadores ausentes são selecionados aleatoriamente. Para criar os novos percentuais, basta digitar:

# Ausência de 2,5% dos Deputados
n_dep_pres <- floor(nrow(new_dep) * 0.975)
dep_pres <- new_dep[sample(seq_len(nrow(new_dep)), n_dep_pres),]

# Ausência de 2,5% dos Senadores
n_sen_pres <- floor(nrow(new_sen) * 0.975)
dep_pres <- new_sen[sample(seq_len(nrow(new_sen)), n_sen_pres),]

# Percentual de favoráveis
n_dep_favor_pres <- length(which(dep_pres == "A favor"))
n_sen_favor_pres <- length(which(sen_pres == "A favor"))
percentual_dep_pres <- n_dep_favor_pres/n_dep
percentual_sen_pres <- n_sen_favor_pres/n_sen
percentual_dep_pres
percentual_sen_pres

O percentual de Deputados favoráveis ao Impeachment quando a abstenção é de 2,5% é de 72,90%, e de Senadores é 51,85%. Para realizar a análise com outras taxas de abstenção basta mudar os percentuais. Ainda assim, a acurácia da previsão depende do fato de que a ausência seja aleatória, e não correlacionada com a intenção de voto, Partido ou Estado.

Atualizando as previsões

Como toda previsão é melhor a medida que incorpora a chegada de novas informações, fiz uma rotina para atualizar os resultados dessa previsão diariamente e publicar na tabela do início deste post.

Tem sugestões para melhorar o algoritmo? Tem dúvidas sobre a implementação? Encontrou algum typo no texto? Me avise nos comentários ou por email.

A árvore do Impeachment

Previsão do resultado do Impeachment brasileiro