O tradeoff entre viés e variância em três gráficos
Entendendo os conceitos de bias-variance tradeoff, underfitting e overfitting através da estimação de diversos modelos de previsão
Ao fazer previsões devemos separar a nossa amostra em uma parte em que estimaremos nosso modelo (train set) e outra parte em que avaliaremos a qualidade da previsão (test set). Quando se trata de escolher o modelo, parâmetros e variáveis a serem utilizadas, nos deparamos com as seguintes opções:
-
Utilizar um modelo complexo que é capaz de reduzir consideravelmente o erro de previsão no train set, mas ao mesmo tempo não é tão generalizável a ponto de apresentar um bom resultado no test set. Nesse caso estamos optando por estimar um modelo com viés baixo e variância alta. Ou seja, no train set, o modelo irá ter um erro de previsão baixo, mas quando avaliamos o modelo em um novo conjunto de dados (test set), o erro sobe consideravelmente, e por isso dizemos que sua variância é alta. Este é o típico caso de overfitting.
-
Utilizar um modelo simples que é bem generalizável, mas não reduz consideravelmente o erro de previsão no train set. Nesse caso estamos optando por um modelo com viés mais alto, mas variância baixa. Assim, iremos permitir um erro de previsão maior no train set de modo a obter um erro de previsão semelhante (com pouca variância) no test set. Esse é o típico caso de underfitting.
Matematicamente, o erro de previsão de um modelo pode ser dado por:
\[E[(y-\hat{f}(x))^2] = Bias[\hat{f}(x)]^2 + Var[\hat{f}(x)] + \sigma^2,\]onde,
\[Bias[\hat{f}(x)] = E[\hat{f}(x) - f(x)],\]e,
\[Var[\hat{f}(x)] = E[\hat{f}(x)^2] - E[\hat{f}(x)]^2.\]Assim, a nossa tarefa é escolher a f(x), sendo que tanto o viés quanto a variância aumenta o erro de previsão. Obviamente a escolha entre 1 e 2 é um tradeoff, e o ideal é permanecermos em um meio termo entre um modelo complexo e bem generalizável. Nesse post faremos um exercício de simulação no R e construiremos três gráficos para entender melhor este tradeoff. Para a construção destes gráficos também estimaremos vários modelos de previsão no R. A primeira etapa é carregar os pacotes necessários (instale-os com install.packages("nomedopacote") caso não os tenha em seu sistema).
library(Metrics) # RMSE function
library(rpart) # CART
library(FNN) # K-nearest neighbour regression
library(e1071) # Support Vector Regression
library(fields) # Thin Plate Spline
library(randomForest) # Random forest
library(xgboost) # Extreme gradient boosting trees
Uma vez instalados os pacotes com os modelos que utilizaremos, vamos simular duas variáveis (x e y) com o objetivo de utilizar a variável x para prever y. Iremos criar uma variável x com variabilidade suficiente e bem espaçada para facilitar a visualização dos gráficos, bem como supor uma relação cúbica entre x e y, adicionando ruídos nessa relação.
# Gerando os dados (relação cúbica entre x e y)
set.seed(123)
x <- seq(-10, 10, length.out=50)
y <- 2*x - 0.5*x^2 + x^3 + rnorm(50, 0, 100)
O tradeoff entre viés e variância (Underfitting e Overfitting)
O primeiro gráfico que construiremos é este:
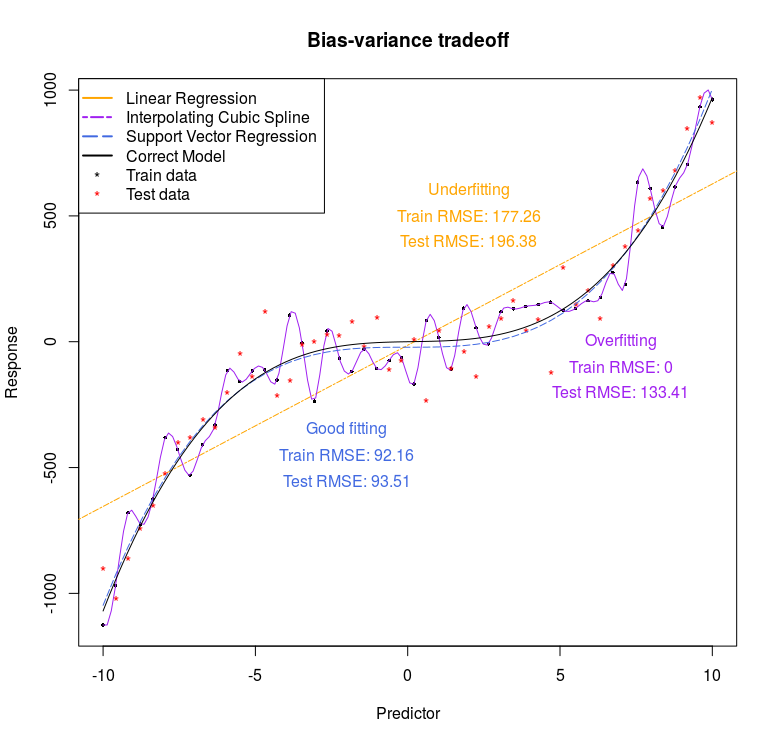
Um dos modelos mais simples que podemos estimar é uma regressão linear através de mínimos quadráticos ordinários, que sabemos que é o melhor estimador linear não viesado. Entretanto estimadores lineares em geral possuem alto viés, pois se distanciam bastante das observações da amostra. A regressão linear será o nosso caso extremo para o item 2 acima, ou seja, um modelo muito simples, mas que pode ser generalizável. Assim, o erro de previsão será alto no train set, e será também alto, mas semelhante, no test set. Este é o típico caso de viés alto e variância baixa, ou underfitting.
Podemos também pensar num modelo bem mais complexo, que passe por todos os pontos do train set, ou seja, uma interpolação. Esse modelo pode ser obtido através de um spline cúbico, e será o caso extremo do item 1 acima. Obviamente, o erro de previsão será zero no train set, mas quando considerarmos os dados novos do test set o erro de previsão será bem mais alto. Este é o típico caso de viés baixo e variância alta, ou overfitting.
Bom, para gerar o gráfico acima, começamos plotando um gráfico com as variáveis x e y e o valor previsto para estes dois modelos.
# Plot data
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "Bias-variance tradeoff")
# Linear regression
reg <- lm(y ~ x)
summary(reg)
abline(reg, col = "orange", lty = 6)
# Interpolating cubic spline
lines(spline(x, y), col = "purple", lty = 1)
Agora vamos adicionar novos pontos em vermelho gerados pelo mesmo processo, interpretando-os como se fosse o nosso test set. Com isso veremos como a interpolação cúbica se distancia desses novos pontos, fazendo com que o erro de previsão seja grande nesse test set.
# Plot new test set
set.seed(321)
y_new <- 2*x - 0.5*x^2 + x^3 + rnorm(50, 0, 100)
points(x, y_new, col = "red", pch = "*")
Gostaríamos de um modelo que estivesse no meio termo do tradeoff viés-variância. Para isso utilizaremos um support vector regression com kernel polinomial. Também incluimos o modelo correto através da função curve (note que em uma aplicação real nunca saberemos este modelo correto). Comparando o nosso modelo com o função geradora dos dados (na curva preta), vemos que ele faz um excelente trabalho.
# Support vector regression com kernel polynomial
svmreg <- svm(y ~ x, kernel = "polynomial")
svmpred <- predict(svmreg, x)
lines(x, svmpred, col = "royalblue", lty = 5)
# Modelo correto
curve(2*x - 0.5*x^2 + x^3, min(x), max(x), add = TRUE)
Ainda falta incluir as legendas:
# Add legend
legend("topleft",
c("Linear Regression", "Interpolating Cubic Spline",
"Support Vector Regression", "Correct Model",
"Train data", "Test data"),
col=c("orange", "purple", "royalblue", "black", "black", "red"),
lty = c(1, 6, 5, 1, NA, NA), pch = c(NA, NA, NA, NA, "*", "*"),
lwd = 2)
Por fim, calculamos a raíz do erro quadrático médio de previsão nos conjuntos test e train, incluindo essa informação no gráfico na forma de texto. Note como nos modelos simples, ambos os erros são altos (underfitting), enquanto que nos modelos complexos o erro no train set é baixo mas no test set é alto. O ideal é que ambos se aproximem, mas na prática sempre queremos minimizar o erro no test set pois estes são os dados novos em que avaliaremos nossa previsão.
# Calcular RMSEs
rmse.reg <- rmse(y, predict(reg, data.frame(x)))
rmse.spline <- rmse(y, spline(x, y, n = 50)$y)
rmse.svm <- rmse(y, svmpred)
rmse.reg.test <- rmse(y_new, predict(reg, data.frame(x)))
rmse.spline.test <- rmse(y_new, spline(x, y, n = 50)$y)
rmse.svm.test <- rmse(y_new, svmpred)
# Adicionar RMSEs ao gráfico
text(2, 600, "Underfitting", col = "orange")
text(2, 500, paste("Train RMSE:",
round(rmse.reg, digits = 2)), col = "orange")
text(2, 400, paste("Test RMSE:",
round(rmse.reg.test, digits = 2)), col = "orange")
text(7, 0, "Overfitting", col = "purple")
text(7, -100, paste("Train RMSE:",
round(rmse.spline, digits = 2)), col = "purple")
text(7, -200, paste("Test RMSE:",
round(rmse.spline.test, digits = 2)), col = "purple")
text(-2, -350, "Good fitting", col = "royalblue")
text(-2, -450, paste("Train RMSE:",
round(rmse.svm, digits = 2)), col = "royalblue")
text(-2, -550, paste("Test RMSE:",
round(rmse.svm.test, digits = 2)), col = "royalblue")
Tradeoff entre viés e variância em vários modelos de previsão
A ideia até aqui é que modelos mais simples tem viés alto mas variância baixa (underfitting), enquanto que modelos mais complexos tem viés baixo mas variância alta (overfitting). Mas o que significa um modelo ser mais complexo? Em geral, a complexidade de um modelo aumenta conforme o número de previsores aumenta, e conforme a capacidade do modelo de captar relações não lineares e interações entre os previsores aumenta. Como nosso exemplo tem apenas um previsor, iremos adicionar complexidade através da não linearidade. Em caso de inúmeros previsores, até mesmo um modelo de regressão linear pode se tornar complexo demais, exigindo técnicas de regularização como LASSO ou Ridge Regression para diminuir a possibilidade de overfitting. Para exemplificar o conceito de tradeoff entre viés e variância, bem como de underfitting e overfitting vamos estimar uma série de modelos com grau crescente de complexidade. O objetivo é gerar o seguinte gráfico:
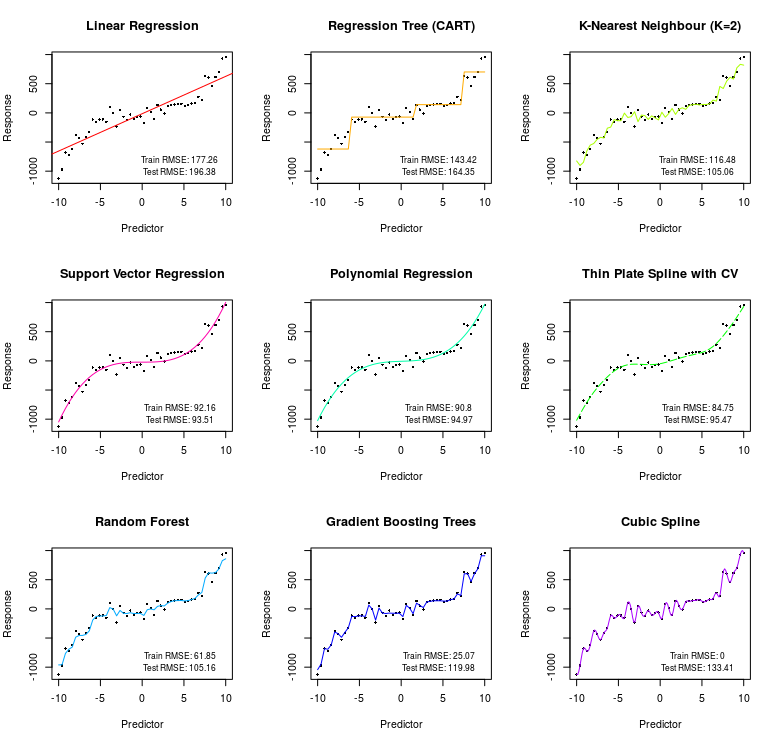
O código com a estimação, previsão e o plot dos gráficos para cada modelo se encontra abaixo. No gráfico, estimamos 9 modelos distintos:
-
O primeiro modelo é a Regressão Linear, que possui alto viés e baixa variância, de modo que os erros do train e test set são altos mas semelhantes.
-
O segundo modelo é o CART, de regressão com árvores. A ideia é estimar uma constante para diferentes níveis da variável previsora
x. Esse modelo diminui um pouco os erros no train e test set, mas ainda assim, no nosso caso, o viés é alto. -
O terceiro modelo é o K-nearest neighbour com K=2. Este é um modelo não-paramétrico que calcula a distância do ponto a ser previsto em relação aos outros pontos da amostra, e utiliza a média dos 2 pontos mais próximos como previsor. Este modelo diminui consideravelmente os erros do train e test set, entretanto ele parece não realizar uma boa previsão nos valores extremos de
x, visto que ao calcular a média dos vizinhos mais próximos a relação polinomial se perde nos extremos. -
O quarto modelo é o Support Vector Regression com kernel polinomial. Este modelo é o que faz o melhor trabalho como previsor, o que é de se esperar, visto que a função geradora dos dados é polinomial.
-
O quinto modelo é uma Regressão Polinomial, que obviamente também faz um excelente trabalho de previsão, visto que a função que gerou os dados é um polinômio.
-
O sexto modelo é um Thin Plate Spline, onde suavizamos a interpolação escolhendo o parâmetro de suavização através de validação cruzada (CV). Este modelo também consegue captar adequadamente a relação polinomial, embora ele tenha um erro no test set um pouco mais alto que os dois anteriores e o erro no train set um pouco mais baixo, indicando o início de um overfitting.
-
O sétimo modelo é um Random Forest, que constrõe diversas árvores completas no estilo do modelo CART reordenando os dados através de um algoritmo de bootstrap, e então utiliza a média delas para diminuir a possibilidade de overfitting. A esta estratégia se dá o nome de Bagging. Entretanto, no nosso caso, o modelo ainda assim passa do ponto ideal, tendo um erro no test set um pouco maior do que os quatro modelos anteriores, apesar de ter o menor erro no train set. Isso indica que o modelo está incorrendo em overfitting.
-
O oitavo modelo é o Gradient Boosting Trees, implementado através do pacote
xgboostdo R. Este é um dos modelos mais utilizados para previsão hoje em dia por sua flexibilidade e adaptabilidade a diferentes problemas. A ideia do modelo é estimar diversas árvores como no modelo CART, mas ao invés de estimar árvores completas e tirar a média como no Random Forest, o modelo começa estimando uma árvore simples, e então utiliza os pontos em que esta árvore não faz um bom trabalho de previsão para estimar outra árvore simples, e assim por diante. A esta estratégia se dá o nome de Boosting. A ideia é diminuir o viés, porém em geral este modelo terá uma variância maior do que Random Forest, podendo facilmente incorrer em overfitting, como acontece no nosso caso, em que o erro no train set é bem baixo, mas no test set é bem maior. -
O último modelo é a interpolação com Spline Cúbico, que passa exatamente por todos os pontos do train set, zerando o erro de previsão. Entretanto, ao avaliar a qualidade da previsão no test set obtemos um erro bem maior. Esse modelo está ocorrendo em um overfitting extremo, sendo complexo demais para gerar uma boa previsão.
Note que dependendo dos dados, os erros do train e test set podem ser completamente diferentes deste gráfico e nem sempre os modelos estarão posicionados exatamente nesta ordem de complexidade do gráfico. Um modelo CART pode ser mais complexo do que um Support Vector Regression, ou até mesmo um Random Forest pode ser mais complexo do que Gradient Boosting Trees, dependendo da parametrização e do conjunto de dados e previsores que se está utilizando. Para o nosso caso, em que o modelo correto é um polinômio, é natural que o Support Vector Regression com kernel polinomial e a Regressão Polinomial apresentem o melhor resultado, mas em geral, com um conjunto de dados mais complexo, com vários previsores, modelos como Random Forest e Gradient Boosting Trees podem ter resultados bem melhores no test set.
# Estimar e plotar 9 modelos diferentes
set.panel(3,3)
## Linear Regression
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "Linear Regression")
reg <- lm(y ~ x)
abline(reg, col = "#FF0000FF")
text(4.5, -800, cex = 0.8,
paste("Train RMSE:",
round(rmse(y, predict(reg, data.frame(x))), digits = 2)))
text(4.5, -1000, cex = 0.8,
paste("Test RMSE:",
round(rmse(y_new, predict(reg, data.frame(x))), digits = 2)))
## Regression Tree (CART)
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "Regression Tree (CART)")
tree <- rpart(y ~ x)
lines(x, predict(tree), col = "#FFAA00FF")
text(4.5, -800, cex = 0.8,
paste("Train RMSE:",
round(rmse(y, predict(tree)), digits = 2)))
text(4.5, -1000, cex = 0.8,
paste("Test RMSE:",
round(rmse(y_new, predict(tree)), digits = 2)))
## K-nearest neighbour
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "K-Nearest Neighbour (K=2)")
knnfit <- knn.reg(train=x, y=y, k = 2)
lines(x, knnfit$pred, col = "#AAFF00FF")
text(4.5, -800, cex = 0.8,
paste("Train RMSE:",
round(rmse(y, knnfit$pred), digits = 2)))
text(4.5, -1000, cex = 0.8,
paste("Test RMSE:",
round(rmse(y_new, knnfit$pred), digits = 2)))
## Support vector regression with polynomial kernel
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "Support Vector Regression")
svmreg <- svm(y ~ x, kernel = "polynomial")
svmpred <- predict(svmreg, x)
lines(x, svmpred, col = "#FF00AAFF")
text(4.5, -800, cex = 0.8,
paste("Train RMSE:",
round(rmse(y, svmpred), digits = 2)))
text(4.5, -1000, cex = 0.8,
paste("Test RMSE:",
round(rmse(y_new, svmpred), digits = 2)))
## Polynomial regression
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "Polynomial Regression")
polyreg <- lm(y ~ poly(x, 3))
lines(x, predict(polyreg, data.frame(x)), col = "#00FFAAFF")
text(4.5, -800, cex = 0.8,
paste("Train RMSE:",
round(rmse(y, predict(polyreg, data.frame(x))), digits = 2)))
text(4.5, -1000, cex = 0.8,
paste("Test RMSE:",
round(rmse(y_new, predict(polyreg, data.frame(x))), digits = 2)))
## Thin plate spline with CV (smoothing)
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "Thin Plate Spline with CV")
tps <- Tps(x, y)
lines(x, predict(tps, x), col = "#00FF00FF", lty = 5)
text(4.5, -800, cex = 0.8,
paste("Train RMSE:",
round(rmse(y, predict(tps, x)), digits = 2)))
text(4.5, -1000, cex = 0.8,
paste("Test RMSE:",
round(rmse(y_new, predict(tps, x)), digits = 2)))
## Random forest
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "Random Forest")
set.seed(123)
rf <- randomForest(y ~ x)
lines(x, predict(rf, x), col = "#00AAFFFF")
text(4.5, -800, cex = 0.8,
paste("Train RMSE:",
round(rmse(y, predict(rf, x)), digits = 2)))
text(4.5, -1000, cex = 0.8,
paste("Test RMSE:",
round(rmse(y_new, predict(rf, x)), digits = 2)))
## Extreme gradient boosting trees
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "Gradient Boosting Trees")
xgb <- xgboost(data = as.matrix(x), label = y, nrounds = 500, eta = 0.01)
lines(x, predict(xgb, as.matrix(x)), col = "#0000FFFF")
text(4.5, -800, cex = 0.8,
paste("Train RMSE:",
round(rmse(y, predict(xgb, as.matrix(x))), digits = 2)))
text(4.5, -1000, cex = 0.8,
paste("Test RMSE:",
round(rmse(y_new, predict(xgb, as.matrix(x))), digits = 2)))
## Interpolating Cubic Spline
plot(x, y, xlim = c(min(x), max(x)), ylim = c(min(y), max(y)), pch=16,
cex = 0.5, ylab = "Response", xlab = "Predictor",
main = "Cubic Spline")
lines(spline(x, y), col = "#AA00FFFF")
text(4.5, -800, cex = 0.8,
paste("Train RMSE:",
round(rmse(y, spline(x, y, n = 50)$y), digits = 2)))
text(4.5, -1000, cex = 0.8,
paste("Test RMSE:",
round(rmse(y_new, spline(x, y, n = 50)$y), digits = 2)))
Erro de previsão no train e test set
Por fim, para resumir a relação entre erro de previsão no train e test set com a complexidade do modelo, podemos gerar o seguinte gráfico:
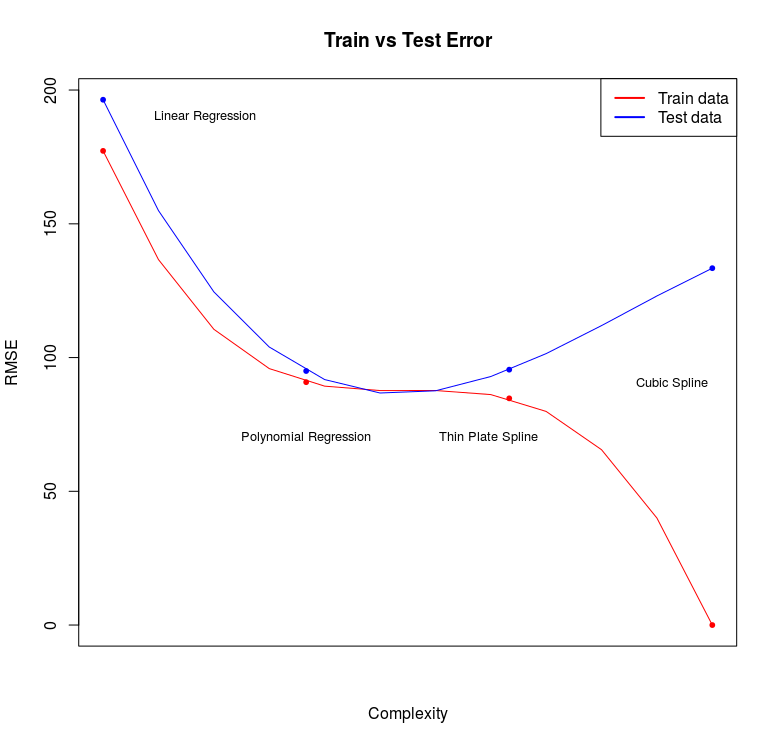
Note que aumentando a complexidade do modelo diminuimos o erro no train e test set até o ponto em que o erro no test set começa aumentar. A partir daí o aumento na variância não compensa a diminuição no viés e nosso modelo passa a ter uma má performance em conjuntos novos de dados. A tarefa essencial de previsão é selecionar um modelo que se aproxime do ponto mínimo da curva de erro do test set. O código para gerar o gráfico encontra-se abaixo:
# Calculando RMSE para alguns modelos no train e test set
RMSE <- data.frame(
Train = c(rmse(y, predict(reg, data.frame(x))),
rmse(y, predict(polyreg, data.frame(x))),
rmse(y, predict(tps, x)),
rmse(y, spline(x, y, n = 50)$y)),
Test = c(rmse(y_new, predict(reg, data.frame(x))),
rmse(y_new, predict(polyreg, data.frame(x))),
rmse(y_new, predict(tps, x)),
rmse(y_new, spline(x, y, n = 50)$y)))
rownames(RMSE) <- c("Linear Regression", "Polynomial Regression",
"Thin Plate Spline", "Cubic Spline")
# Plotando relação entre RMSE e Complexidade dos modelos
dev.new()
plot(RMSE$Train, col = "red", pch = 20, xaxt = "n",
ylim = c(min(RMSE$Train), max(RMSE$Test)),
xlab = "Complexity", ylab = "RMSE",
main = "Train vs Test Error")
points(RMSE$Test, col = "blue", pch = 20)
text(c(1.5, 2.0, 2.9, 3.8), c(190, 70, 70, 90),
labels = rownames(RMSE), cex = 0.8)
lines(spline(1:nrow(RMSE), RMSE$Train), col = "red")
lines(spline(1:nrow(RMSE), RMSE$Test), col = "blue")
legend("topright", c("Train data", "Test data"),
col = c("red", "blue"), lwd=2)